题目
已知向量 \boldsymbol{ a }, \boldsymbol{ b } 满足 | \boldsymbol{ a } | = | \boldsymbol{ b } | = 6 且 \boldsymbol{ a } \perp \boldsymbol{ b },向量 \boldsymbol{ c } 满足 | \boldsymbol{ a } + \boldsymbol{ b } - \boldsymbol{ c } | = 2,求 | \boldsymbol{ a } - \boldsymbol{ c } | + 3 | 2 \boldsymbol{ b } - \boldsymbol{ c } | 的最小值。
解析
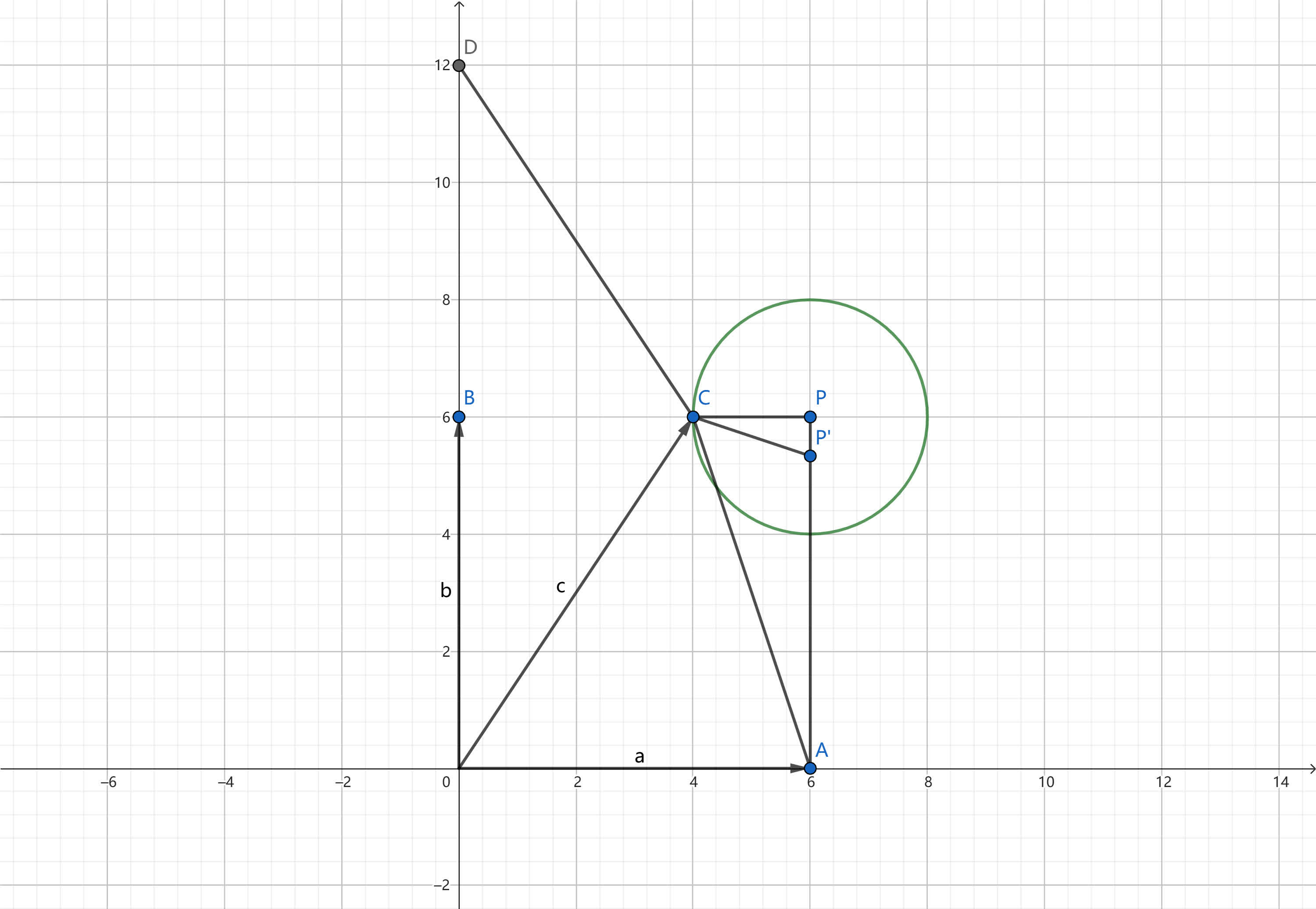
如图建系,则 \boldsymbol{ c } 的终点在以 P ( 6, 6 ) 为圆心,2 为半径的圆上。
作 P' \left ( 6, \dfrac{ 16 }{ 3 } \right ),则因为 \dfrac{ PP' }{ PC } = \dfrac{ PC }{ PA },故 \triangle PCP' \sim \triangle PAC,且 CP' = \dfrac{ 1 }{ 3 } CA。
故 | \boldsymbol{ a } - \boldsymbol{ c } | + 3 | 2 \boldsymbol{ b } - \boldsymbol{ c } | = CA + 3 CD = 3 ( CP' + CD ) \geq 3 DP' = 2 \sqrt{ 181 }。
by CXY。
