题目

在 \triangle ABC 中，AB = \sqrt{ 6 }, AC = \sqrt{ 3 }, \angle BAC = \dfrac{ 5 \mathrm{ \pi } }{ 12 }，点 P 是 \triangle ABC 所在平面内一点，求 \overrightarrow{ PA } \cdot \overrightarrow{ PB } + \overrightarrow{ PA } \cdot \overrightarrow{ PC } 的最小值。

解析

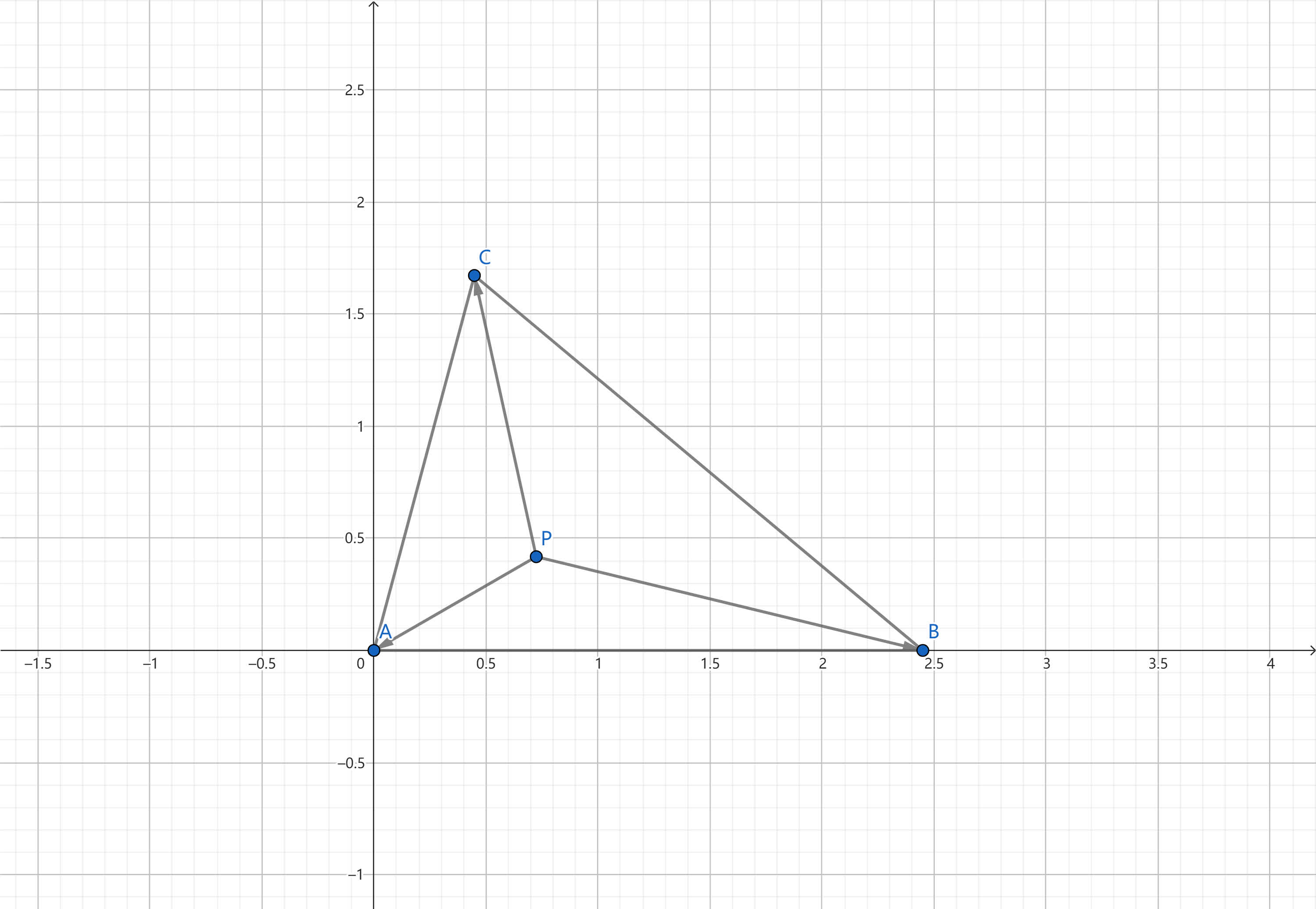
2024-05-08-01

如图建系，则有 A ( 0, 0 ), B \left ( \sqrt{ 6 }, 0 \right ), C \left ( \dfrac{ 3 \sqrt{ 2 } - \sqrt{ 6 } }{ 4 }, \dfrac{ 3 \sqrt{ 2 } + \sqrt{ 6 } }{ 4 } \right )。

设 P ( x, y )，则有 \overrightarrow{ PA } = ( -x, -y ), \overrightarrow{ PB } = \left ( \sqrt{ 6 } - x, -y \right ), \overrightarrow{ PC } = \left ( \dfrac{ 3 \sqrt{ 2 } - \sqrt{ 6 } }{ 4 } - x, \dfrac{ 3 \sqrt{ 2 } + \sqrt{ 6 } }{ 4 } - y \right )。

则有：

\begin{aligned} \overrightarrow{ PA } \cdot \overrightarrow{ PB } + \overrightarrow{ PA } \cdot \overrightarrow{ PC } & = ( -x ) \left ( \sqrt{ 6 } - x \right ) + ( -y )^{ 2 } + ( -x ) \left ( \dfrac{ 3 \sqrt{ 2 } - \sqrt{ 6 } }{ 4 } - x \right ) + ( -y ) \left ( \dfrac{ 3 \sqrt{ 2 } + \sqrt{ 6 } }{ 4 } - y \right ) \\ & = 2 x^{ 2 } - \dfrac{ 3 \sqrt{ 2 } + 3 \sqrt{ 6 } }{ 4 } x + 2 y^{ 2 } - \dfrac{ 3 \sqrt{ 2 } + \sqrt{ 6 } }{ 4 } y \\ & = \left ( \sqrt{ 2 } x - \dfrac{ 3 + 3 \sqrt{ 3 } }{ 8 } \right )^{ 2 } + \left ( \sqrt{ 2 } y - \dfrac{ 3 + \sqrt{ 3 } }{ 8 } \right )^{ 2 } - \dfrac{ 6 + 3 \sqrt{ 3 } }{ 8 } \\ & \geq -\dfrac{ 6 + 3 \sqrt{ 3 } }{ 8 } \end{aligned}

故 \overrightarrow{ PA } \cdot \overrightarrow{ PB } + \overrightarrow{ PA } \cdot \overrightarrow{ PC } 的最小值即为 -\dfrac{ 6 + 3 \sqrt{ 3 } }{ 8 }。

by CXY。