题目
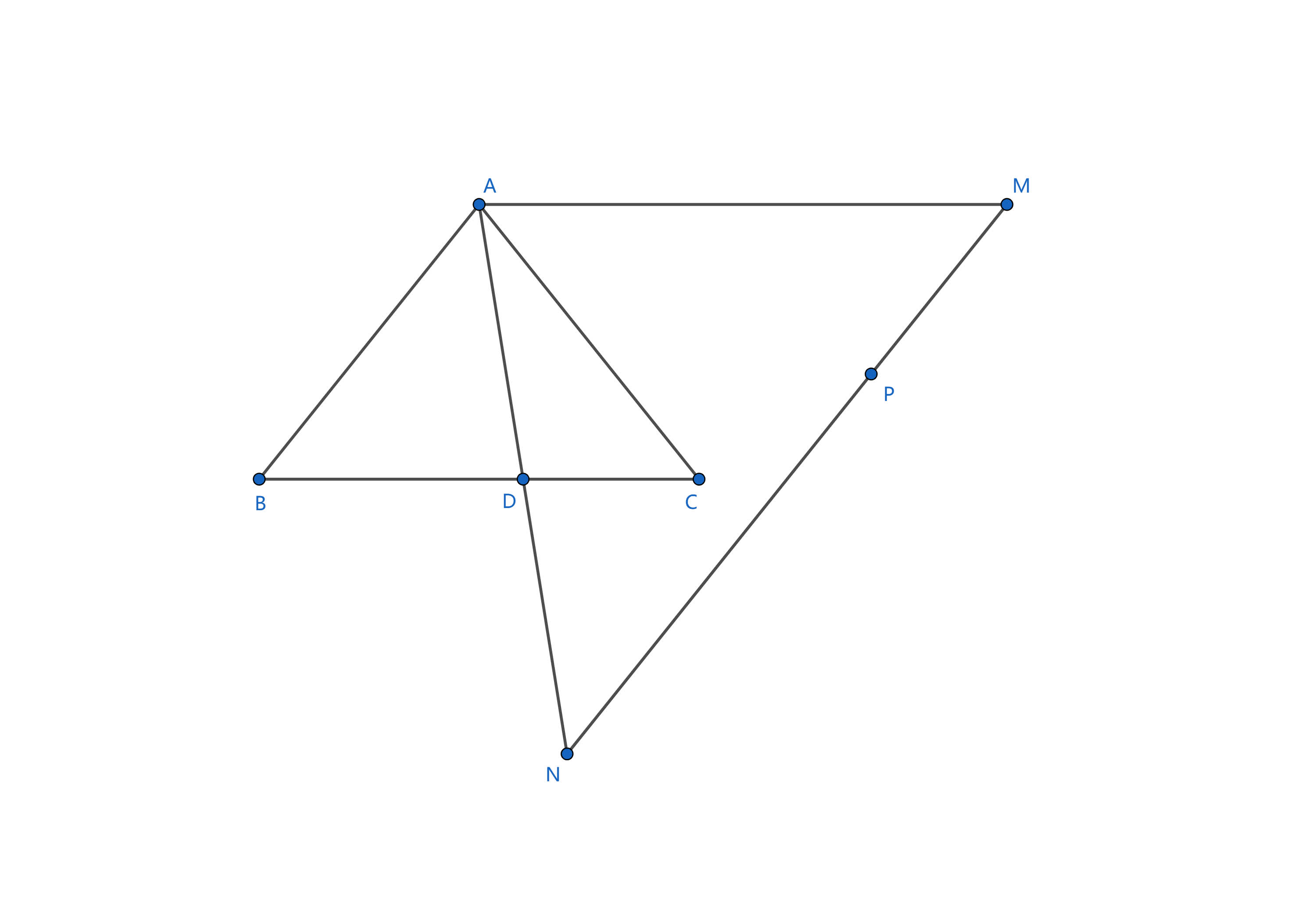
在 \triangle ABC 中,AB = AC = 4, BC = 5 ,D 是线段 BC 上一点且 DC = 2 。若平面上一点 P 满足 \overrightarrow{ AP } = \lambda \overrightarrow{ AD } + \mu \overrightarrow{ BC } (\lambda, \mu \geq 0 ),且 3 \lambda + 5 \mu = 6 ,求点 P 到直线 AB 距离的取值范围。
解析
由于:
\overrightarrow{ AP } = \lambda \overrightarrow{ AD } + \mu \overrightarrow{ BC } = \dfrac{ \lambda }{ 2 } \cdot 2 \overrightarrow{ AD } + \dfrac{ 5 \mu }{ 6 } \cdot \dfrac{ 6 }{ 5 } \overrightarrow{ BC } = \dfrac{ \lambda }{ 2 } \cdot 2 \overrightarrow{ AD } + \left ( 1 - \dfrac{ \lambda }{ 2 } \right ) \cdot \dfrac{ 6 }{ 5 } \overrightarrow{ BC }
不妨令 \overrightarrow{ AM } = 2 \overrightarrow{ AD }, \overrightarrow{ AM } = \dfrac{ 6 }{ 5 } \overrightarrow{ BC } ,则 \overrightarrow{ AP } = \dfrac{ \lambda }{ 2 } \overrightarrow{ AN } + \left ( 1 - \dfrac{ \lambda }{ 2 } \right ) \overrightarrow{ AM } ,即 P 在线段 NM 上。
由于:
\begin{aligned}
\overrightarrow{ MN } & = \overrightarrow{ AN } - \overrightarrow{ AM } \\
& = 2 \overrightarrow{ AD } - \dfrac{ 6 }{ 5 } \overrightarrow{ BC } \\
& = 2 \left ( \overrightarrow{ AB } + \overrightarrow{ BD } \right ) - \dfrac{ 6 }{ 5 } \overrightarrow{ BC } \\
& = 2 \overrightarrow{ AB } + \dfrac{ 6 }{ 5 } \overrightarrow{ BC } - \dfrac{ 6 }{ 5 } \overrightarrow{ BC } \\
& = 2 \overrightarrow{ AB }
\end{aligned}
所以有 \overrightarrow{ MN } 平行于 \overrightarrow{ AB } ,即点 P 到直线 AB 的距离为定值。
由余弦定理可知:
\cos{ \angle ABC } = \dfrac{ AB^{ 2 } + BC^{ 2 } - AC^{ 2 } }{ 2 AB \cdot BC } = \dfrac{ 5 }{ 8 }
故 \sin{ \angle ABC } = \sqrt{ 1 - \cos^{ 2 }{ \angle ABC } } = \dfrac{ \sqrt{ 39 } }{ 8 } 。
故 P 到直线 AB 的距离即为 M 到直线 AB 的距离即为:
d = AM \sin{ \angle ABC } = \dfrac{ 3 \sqrt{ 39 } }{ 4 }
故点 P 到直线 AB 距离的取值范围即为 \left \{ \dfrac{ 3 \sqrt{ 39 } }{ 4 } \right \} 。
by HAR。