题目

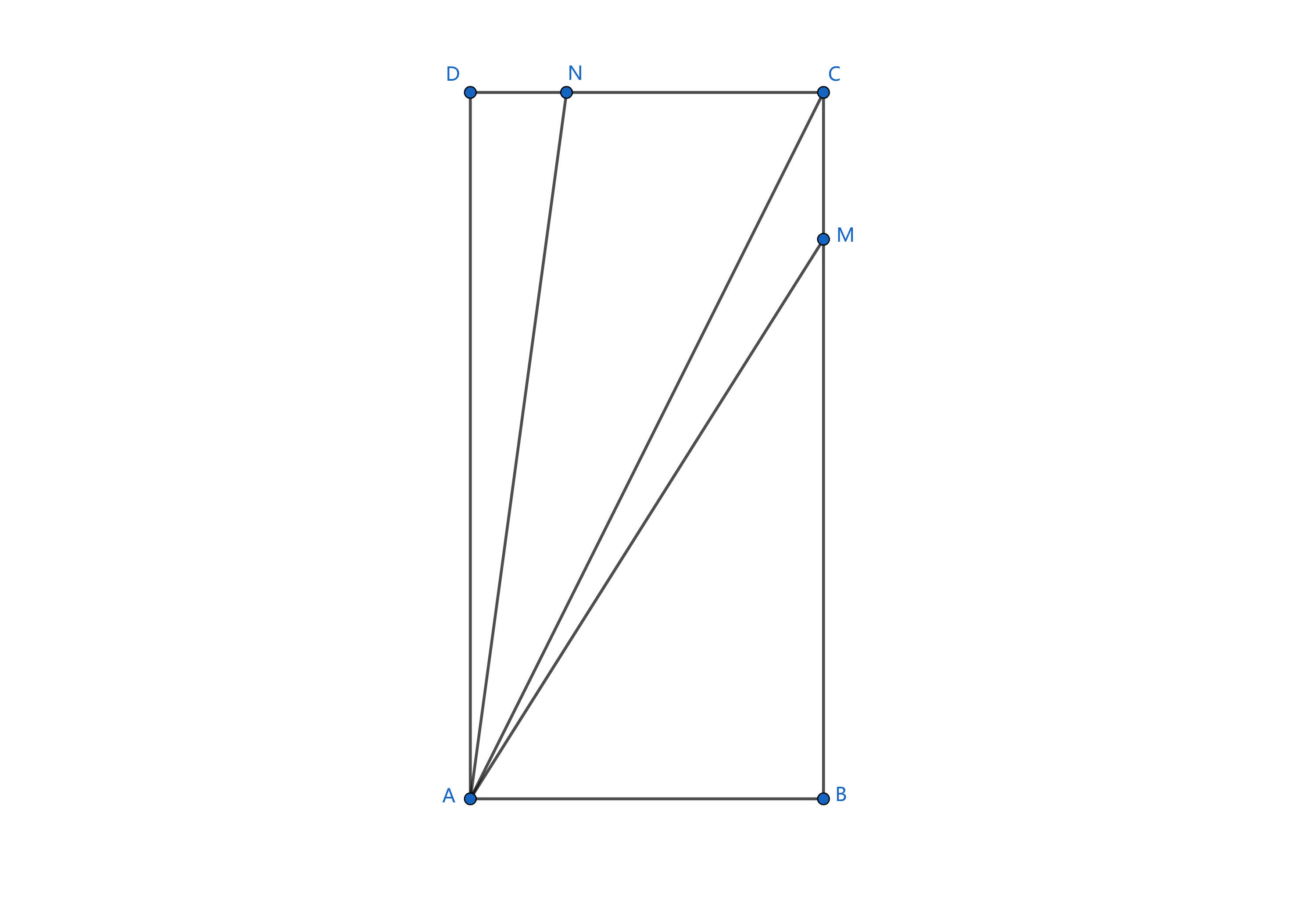
如图所示，在长方形 ABCD 中，有 AB = 2, AD = 4，M, N 分别为 BC, DC 边上的两点，满足 CM^{ 2 } \cdot CN = 1。若有 \overrightarrow{ AC } = x \overrightarrow{ AM } + y \overrightarrow{ AN }，求 x + y 的最大值。

2024-03-05-01

解析

设 CM = \lambda, CN = \mu，则有 \mu = \dfrac{ 1 }{ \lambda^{ 2 } }。

因为有 \overrightarrow{ AC } = \overrightarrow{ AB } + \overrightarrow{ AD }，且有：

\begin{aligned} \overrightarrow{ AC } & = x \overrightarrow{ AM } + y \overrightarrow{ AN } \\ & = x \left ( \overrightarrow{ AB } + \overrightarrow{ BM } \right ) + y \left ( \overrightarrow{ AD } + \overrightarrow{ DN } \right ) \\ & = \left ( x + y - \dfrac{ \mu }{ 2 } y \right ) \overrightarrow{ AB } + \left ( x + y - \dfrac{ \lambda }{ 4 } x \right ) \overrightarrow{ AD } \end{aligned}

故有：

x + y - \dfrac{ \mu }{ 2 } y = x + y - \dfrac{ \lambda }{ 4 } x = 1

可以解得 x = \dfrac{ \dfrac{ 4 }{ \lambda } }{ \dfrac{ 4 }{ \lambda } + \dfrac{ 2 }{ \mu } - 1 }, y = \dfrac{ \dfrac{ 2 }{ \mu } }{ \dfrac{ 4 }{ \lambda } + \dfrac{ 2 }{ \mu } - 1 }。故 x + y = 1 + \dfrac{ 1 }{ \dfrac{ 4 }{ \lambda } + \dfrac{ 2 }{ \mu } - 1 }。

由于 \dfrac{ 4 }{ \lambda } + \dfrac{ 2 }{ \mu } = \dfrac{ 4 }{ \lambda } + 2 \lambda^{ 2 } \geq 3 \sqrt[ 3 ]{ \dfrac{ 2 }{ \lambda } \cdot \dfrac{ 2 }{ \lambda } \cdot 2 \lambda^{ 2 } } = 6，故 x + y \leq 1 + \dfrac{ 1 }{ 6 - 1 } = \dfrac{ 6 }{ 5 }。

by CXY。