题目
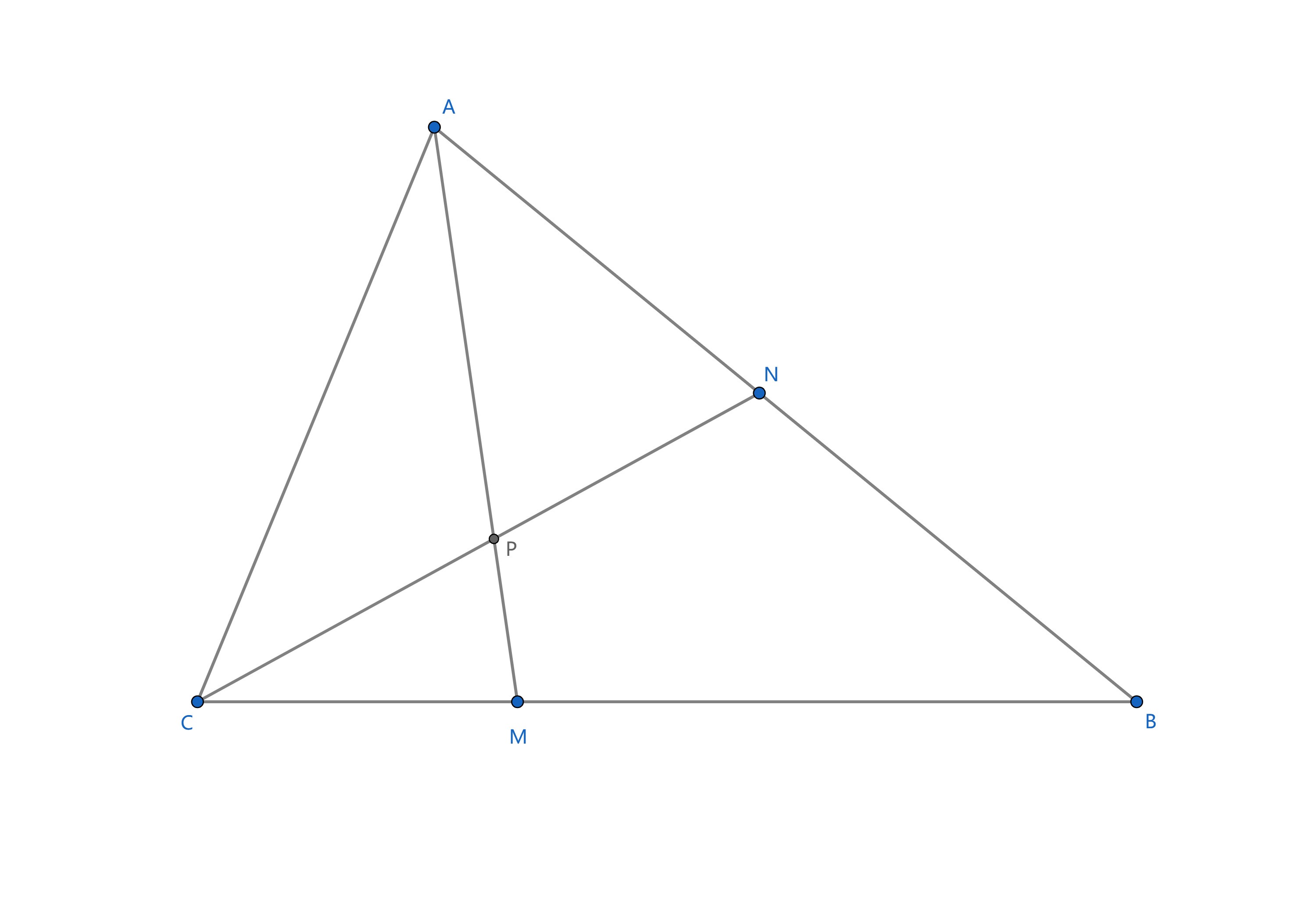
如图,在 \triangle ABC 中,N 为线段 AB 上一点,满足 \overrightarrow{ AN } = \alpha \overrightarrow{ NB },M 为 BC 上一点,满足 \overrightarrow{ CM } = 2 \alpha^{ 3 } \overrightarrow{ MB },线段 CN 与线段 AM 交于点 P。求当 \alpha 变化时,\dfrac{ AP }{ PM } 的最小值。
解析
设向量 \boldsymbol{ a } = \overrightarrow{ CA }, \boldsymbol{ b } = \overrightarrow{ CB }。
则 \overrightarrow{ AB } = \boldsymbol{ b } - \boldsymbol{ a }, \overrightarrow{ AN } = \dfrac{ \alpha }{ \alpha + 1 } ( \boldsymbol{ b } - \boldsymbol{ a } ),则有 \overrightarrow{ CN } = \overrightarrow{ CA } + \overrightarrow{ AN } = \dfrac{ 1 }{ \alpha + 1 } \boldsymbol{ a } + \dfrac{ \alpha }{ \alpha + 1 } \boldsymbol{ b }。
则 \overrightarrow{ CM } = \dfrac{ 2 \alpha^{ 3 } }{ 2 \alpha^{ 3 } + 1 } \boldsymbol{ b },则有 \overrightarrow{ AM } = \overrightarrow{ CM } - \overrightarrow{ CA } = \dfrac{ 2 \alpha^{ 3 } }{ 2 \alpha^{ 3 } + 1 } \boldsymbol{ b } - \boldsymbol{ a }。
设 \dfrac{ AP }{ PM } = \lambda,即 \overrightarrow{ AP } = \lambda \overrightarrow{ PM },则有 \overrightarrow{ AP } = \dfrac{ \lambda }{ \lambda + 1 } \overrightarrow{ AM } = \dfrac{ \lambda }{ \lambda + 1 } \cdot \dfrac{ 2 \alpha^{ 3 } }{ 2 \alpha^{ 3 } + 1 } \boldsymbol{ b } - \dfrac{ \lambda }{ \lambda + 1 } \boldsymbol{ a }。
则 \overrightarrow{ CP } = \overrightarrow{ CA } + \overrightarrow{ AP } = \dfrac{ 1 }{ \lambda + 1 } \boldsymbol{ a } + \dfrac{ \lambda }{ \lambda + 1 } \cdot \dfrac{ 2 \alpha^{ 3 } }{ 2 \alpha^{ 3 } + 1 } \boldsymbol{ b }。
由于 \boldsymbol{ a } 与 \boldsymbol{ b } 不共线,且 C, P, N 三点共线,所以有:
可以解得 \lambda = \alpha + \dfrac{ 1 }{ 2 \alpha^{ 2 } } \geq 3 \sqrt[ 3 ]{ \dfrac{ \alpha }{ 2 } \cdot \dfrac{ \alpha }{ 2 } \cdot \dfrac{ 1 }{ 2 \alpha^{ 2 } } } = \dfrac{ 3 }{ 2 },此时 \alpha = 1。
by CXY。
