题目
某游乐场内有一个供人们游玩的游乐设施。
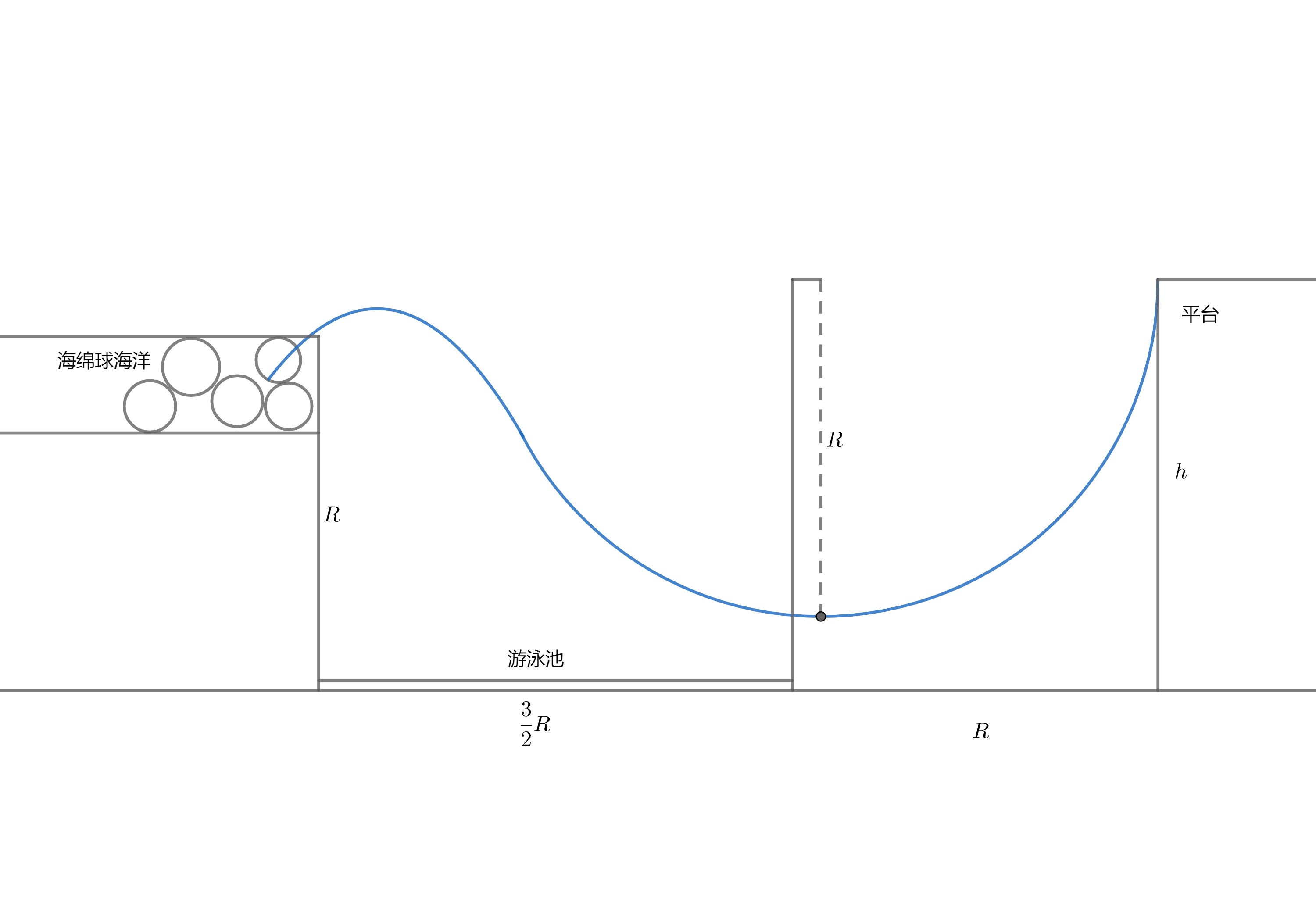
如图所示,该设施由三大部分组成,分别为辅助秋千,长方形河道形游泳池与长方形海绵球海洋组成。
其中辅助秋千为一长为 R 且不可伸长的细绳,其上端固定于固定装置上,下端绑上座位。河道形游泳池宽为 1.5 R,长足够长,游泳池一侧有海绵球海洋,长与宽均足够大,海绵球海洋高比游泳池高 R,游泳池另一侧置有辅助秋千。
游客可以从与辅助秋千等高、与河道形游泳池分布在辅助秋千两侧,边缘距辅助秋千距离为 R 的向后延伸的平台上抓住绳结后离开平台,在绳的约束下做轨迹为部分圆周的运动,当其经过最低点后到达辅助秋千另一侧,绳与竖直方向成一定角度时松手做斜抛运动,落入海绵球海洋或游泳池。
试问:若要使游客有可能落入海绵球海洋,h 最小为多少?
本题可使用计算器,R 为已知,忽略无关因素,游客视为质点,g 取 10 \mathrm{ m / s^{ 2 } },答案保留十位有效数字。
解析
由题,游客的运动总共分为抓绳时的变速圆周运动与松手后的抛体运动两部分组成。由于在抓绳时,游客受绳的拉力与自身重力,而绳的拉力始终垂直于游客运动方向,并且在松手后游客仅受自身重力,所以整个研究过程中只有重力对游客做功,故游客机械能守恒。
假设游客在绳与竖直方向夹角为 \theta 时松手,由题目可知此时游客在装置偏向游泳池一侧。取地面为重力势能的零势能点,由初末态机械能守恒可知游客松手时的速度 v 满足:
故有 v = \sqrt{ 2 g R \cos{ \theta } }。
对于一个初速度为 v_{ 0 },与水平方向夹角为 \theta 的斜抛运动,设出发点为原点,易得小球的运动轨迹为:
y = -\dfrac{ g x^{ 2 } }{ 2 { v_{ 0 } }^{ 2 } \cos^{ 2 }{ \theta } } + x \tan{ \theta }
以绳系在固定装置上的点为坐标原点,向上、向游泳池方向为正方向,可得出游客在绳与竖直方向夹角成任意 \theta(\theta \in ( 0, \dfrac{ \mathrm{ \pi } }{ 2 } ))时松手,当游客到达距原点水平距离为 \dfrac{ 3 }{ 2 } R 时,其纵坐标为:
对其求导可得:
求解 y' ( \theta_{ 0 } ) = 0 可解得 \theta_{ 0 } = \arctan{ \sqrt{ \dfrac{ 7 + 3 \sqrt{ 41 } }{ 10 } } } \approx 1.017469770。
故可知 y ( \theta ) \in ( -\infty, y ( \theta_{ 0 } ) ),此处可以求得 y ( \theta_{ 0 } ) = -\sqrt{ \dfrac{ 123 \sqrt{ 41 } - 767 }{ 512 } } \approx -0.2005085390。
所以有 h \geq R - y ( \theta_{ 0 } ) \approx 1.2005085390 R。
by ZTH。
