题目
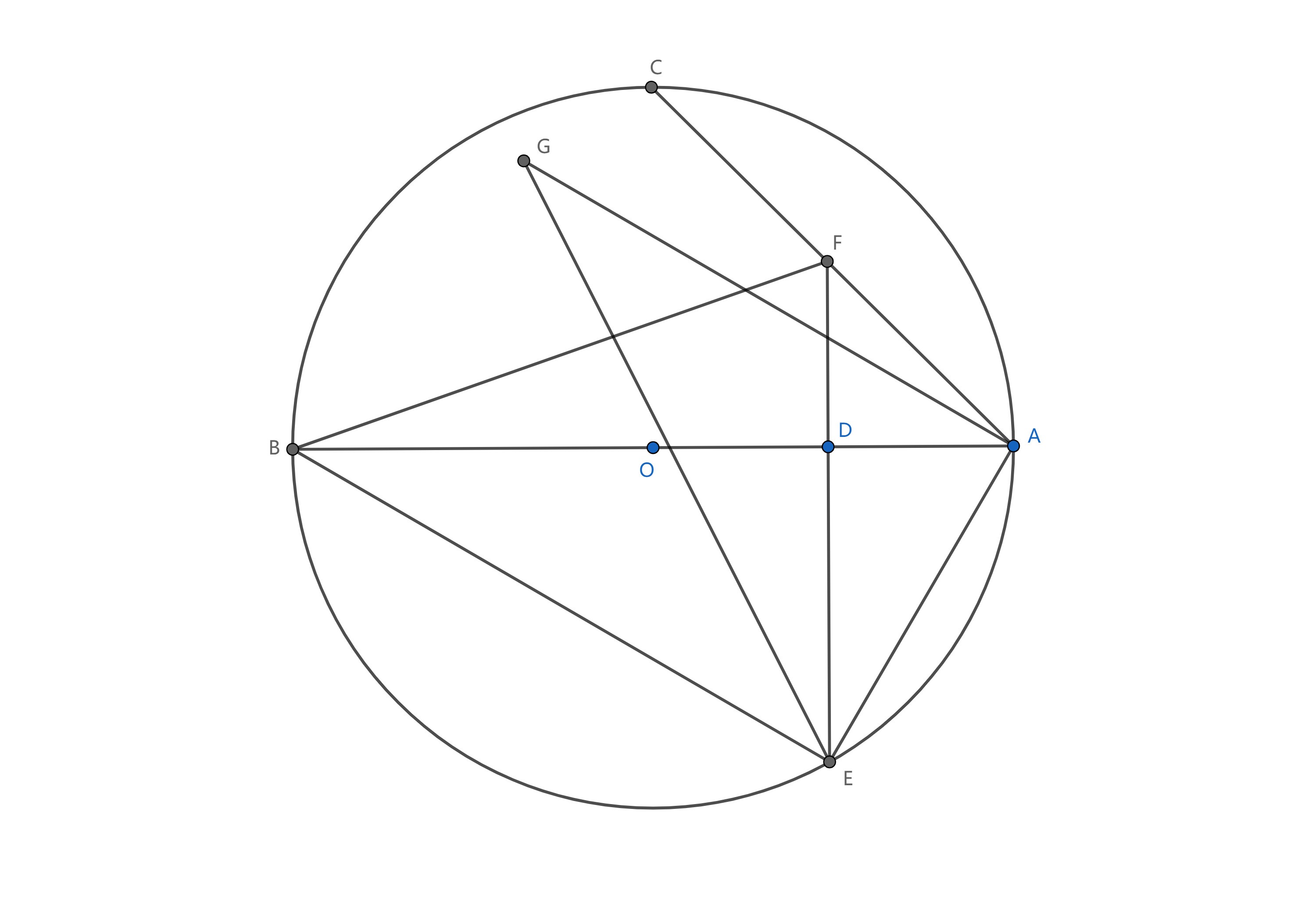
如图,AB 是 \odot O 的直径,\angle{ BAC } = 45 \degree,D 是半径 OA 上的一动点,DE \perp AB 交 \odot O 于点 E,交 AC 于点 F,过 A 做 BE 的平行线 AG 且满足 AG = BF。求证:S_{ \triangle AEG } \geq S_{ \triangle BDE } + S_{ \triangle ADF }。
解析
以 D 为原点,DA 方向为 x 轴正半轴,DF 方向为 y 轴正半轴如图建立平面直角坐标系。设 AO = 1, AD = t。
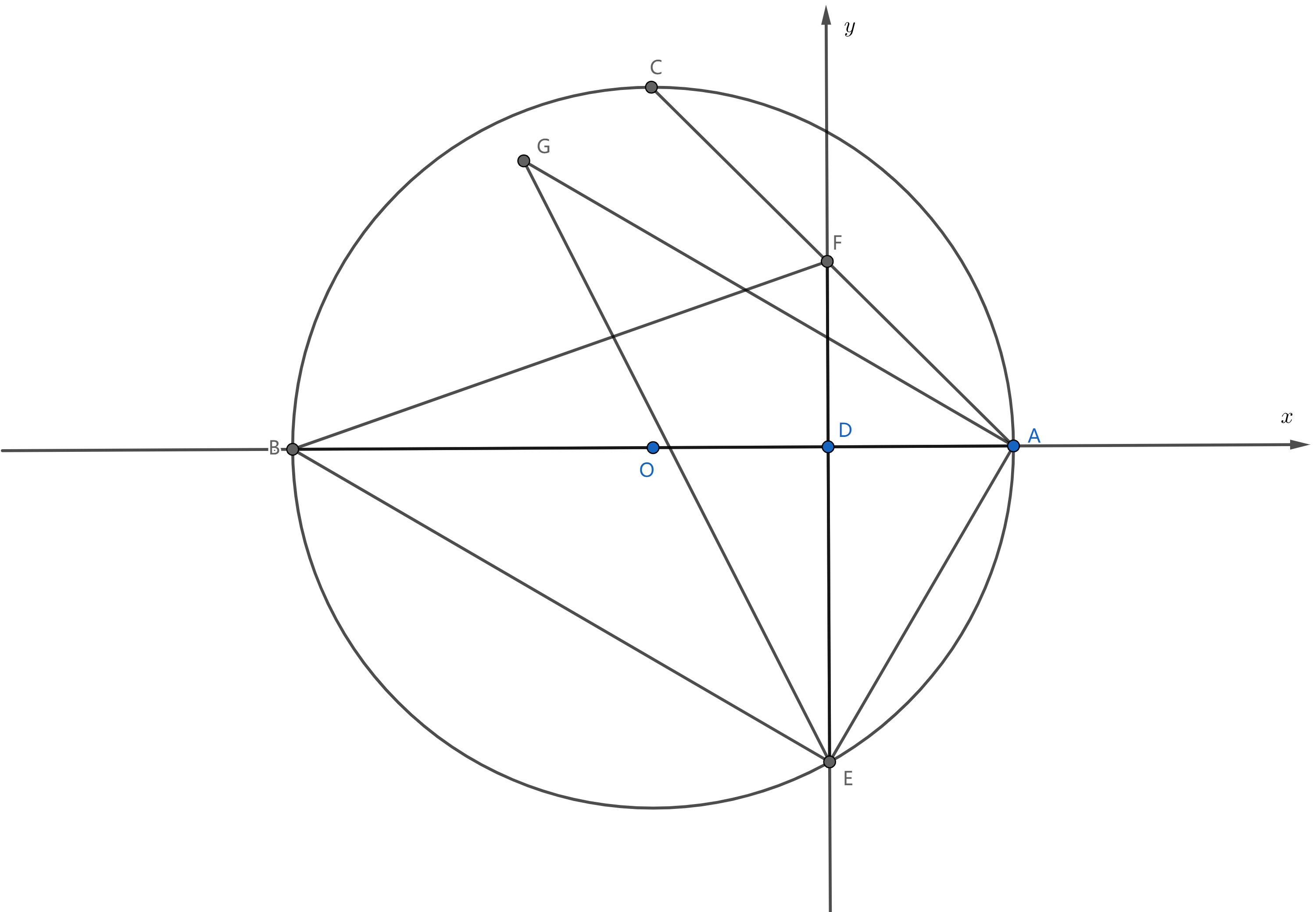
因为有 AD = AF,所以有 l_{ AF } : y = -x + t 且有 F ( 0, t )。因为有 ep_{ \odot O } : ( x - t + 1 )^{ 2 } + y^{ 2 } = 1 且 E 是 \odot O 与 y 轴负半轴的交点,所以联立可以解得 E ( 0, \sqrt{ 2 t - t^{ 2 } } )。
所以有 S_{ \triangle BDE } = \dfrac{ 1 }{ 2 } ( 2 - t ) \sqrt{ 2 t - t^{ 2 } }, S_{ \triangle ADF } = \dfrac{ 1 }{ 2 } t^{ 2 }。
而又有 AE = \sqrt{ t^{ 2 } + \left ( \sqrt{ 2 t - t^{ 2 } } \right )^{ 2 } }, AG = BF = \sqrt{ t^{ 2 } + \left ( 2 - t \right )^{ 2 } },故由柯西不等式可知 S_{ \triangle AEG } = \dfrac{ 1 }{ 2 } \cdot \sqrt{ t^{ 2 } + \left ( \sqrt{ 2 t - t^{ 2 } } \right )^{ 2 } } \cdot \sqrt{ t^{ 2 } + \left ( 2 - t \right )^{ 2 } } \geq \dfrac{ 1 }{ 2 } \left ( t^{ 2 } + ( 2 - t ) \sqrt{ 2 t - t^{ 2 } } \right ) = S_{ \triangle BDE } + S_{ \triangle ADF }。故得证。
by HAR。
