题目
你要选择一组 ( a, b ) 满足以下条件:
- a + b \leq \dfrac{ \sqrt{ 2 } }{ 2 }
- a - \sqrt{ 3 } b \leq \sqrt{ 3 }
- b - a \leq 1
不过你很懒,只会从 \{ ( a, b ) | a^2 + b^2 \leq 1 \} 中随机选择一个 ( a, b ),试问这样选出来的这组数满足上述条件的概率是多少。
解析
答案即为满足 x + y \leq \dfrac{ \sqrt{ 2 } }{ 2 }, x - \sqrt{ 3 } y \leq \sqrt{ 3 }, y - x \leq 1, x^{ 2 } + y^{ 2 } \leq 1 的图形的面积与满足 x^{ 2 } + y^{ 2 } \leq 1 的图形的面积的比,记前者的面积为 S_{ 1 },后者的面积为 S_{ 2 },则不难发现 S_{ 2 } = \mathrm{ \pi }。
考虑如何求 S_{ 1 },可以先画出图像:
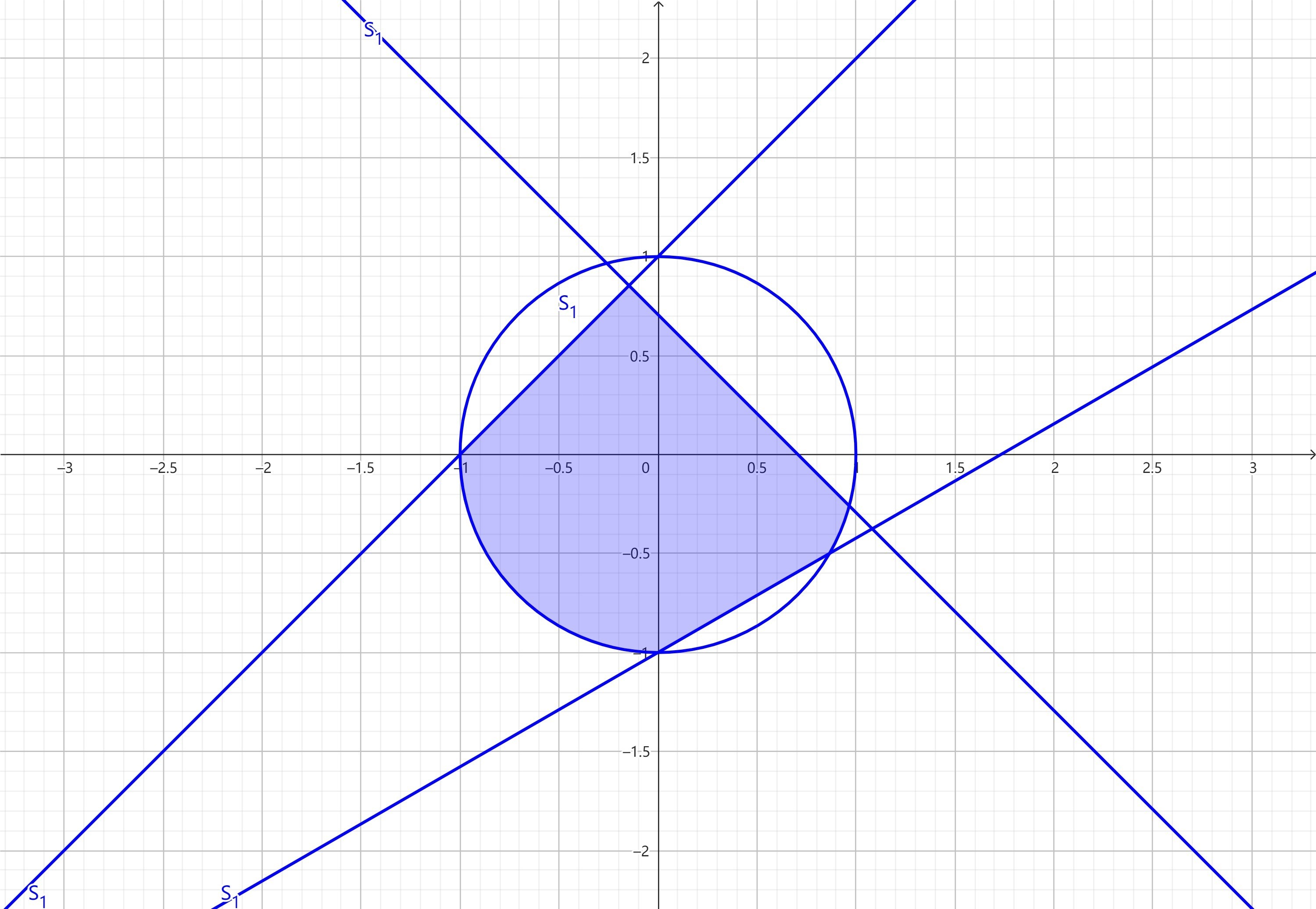
利用扇形面积和三角形面积差,经过分块运算,可以求得 S_{ 1 } = \dfrac{ 6 + 6 \sqrt{ 2 } + 9 \sqrt{ 3 } + 7 \mathrm{ \pi } }{ 24 }。
所以答案即为 \dfrac{ S_{ 1 } }{ S_{ 2 } } = \dfrac{ 6 + 6 \sqrt{ 2 } + 9 \sqrt{ 3 } + 7 \mathrm{ \pi } }{ 24 \mathrm{ \pi } }(该值约为 0.690532)。
by CXY。
