题目
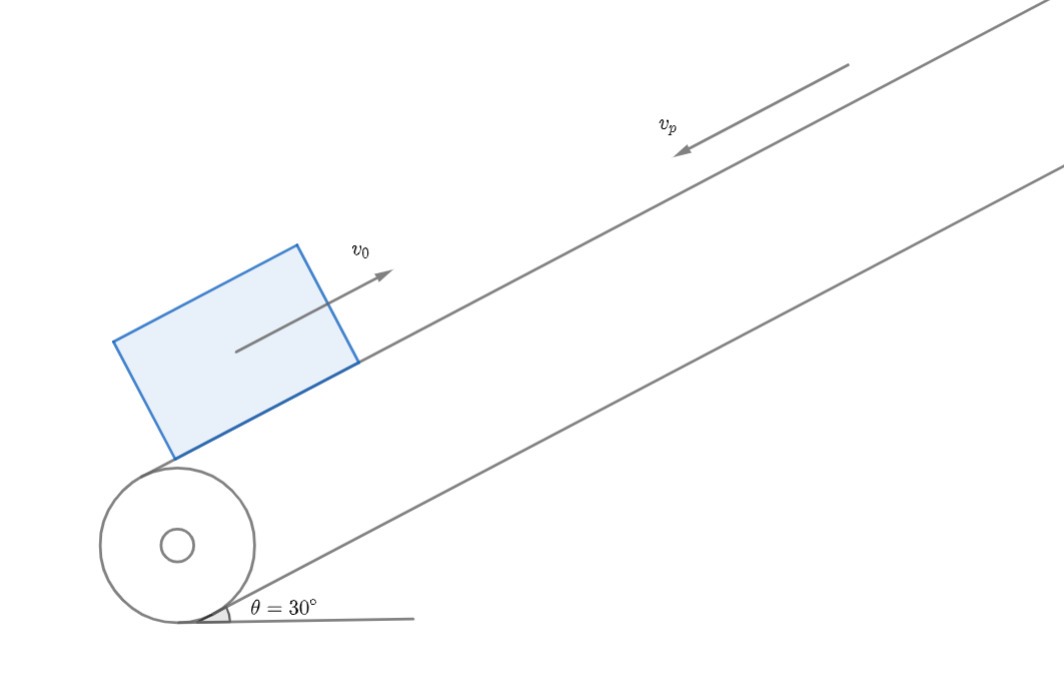
如图有一条无限长的传送带,传送带的速度 v_{ p } = 10 \mathrm{ m / s },沿斜面向下。
在传送带底部轻放一滑块(可视为质点),滑块初速度为 v_{ 0 } = 20 \mathrm{ m / s },沿斜面向上。
当滑块在传送带上滑动且未在滑痕上时,动摩擦因数 \mu = 0.1,每滑动 1 \mathrm{ m },质量变为原来的 \lambda = 0.99 倍。
当在滑痕上滑动时,动摩擦因数 \mu' = 0.05,且滑动时不损失质量。
试求:
- 滑块能到达的高度 h;
- 滑块回到原处的时间 t;
- 传送带上的滑痕长度 \mathrm{ \Delta } x;
- 滑块剩余动能与初始动能的比值 \gamma(百分比形式)。
其中动能可以用 E_{ k } = \dfrac{ 1 }{ 2 } m v^{ 2 } 计算。
本题可以使用计算器,本题均保留两位小数。
解析
滑块向上滑时,其所受摩擦力沿斜面向下,则加速度为 a_{ 1 } = g \sin{ \theta } + \mu g \cos{ \theta } = \dfrac{ 10 + \sqrt{ 3 } }{ 2 } \mathrm{ m / s^{ 2 } }。
故滑块静止时(即达到最大高度时)经过的时间为 t_{ 1 } = \dfrac{ v_{ 0 } }{ a_{ 1 } } = \dfrac{ 400 - 40 \sqrt{ 3 } }{ 97 } \mathrm{ s },经过的路程为 s_{ 1 } = \dfrac{ v_{ 0 }^{ 2 } }{ 2 a_{ 1 } } = \dfrac{ 4000 - 400 \sqrt{ 3 } }{ 97 } \mathrm{ m }。
故 h = s_{ 1 } \sin{ \theta } = \dfrac{ 2000 - 200 \sqrt{ 3 } }{ 97 } \mathrm{ m } \approx 17.05 \mathrm{ m }。
滑块向下滑时,当 v = v_{ p } 时开始在滑痕上滑动,此前经过的时间 t_{ 2 } = \dfrac{ v_{ p } }{ a_{ 1 } } = \dfrac{ 200 - 20 \sqrt{ 3 } }{ 97 } \mathrm{ s },经过的路程 s_{ 2 } = \dfrac{ v_{ p }^{ 2 } }{ 2 a_{ 1 } } = \dfrac{ 1000 - 100 \sqrt{ 3 } }{ 97 } \mathrm{ m }。
当滑块在痕迹上滑动时,摩擦力沿斜面向上,有 a_{ 2 } = g \sin{ \theta } - \mu' g \cos{ \theta } = \dfrac{ 20 - \sqrt{ 3 } }{ 4 } \mathrm{ m / s^{ 2 } }。
滑块在滑痕上滑动的总路程 s_{ 3 } = s_{ 1 } - s_{ 2 } = \dfrac{ 3000 - 300 \sqrt{ 3 } }{ 97 } \mathrm{ m },故滑块到传送带底端时的速度 v_t 满足 v_t^{ 2 } - v_{ p }^{ 2 } = 2 a_{ 2 } s_{ 3 },故 v_t = \sqrt{ 2 a_{ 2 } s_{ 3 } + v_{ p }^{ 2 } } = \dfrac{ \sqrt{ 3894550 - 436500 \sqrt{ 3 } } } { 97 } \mathrm{ m / s },这一段经过的时间为 t_{ 3 } = \dfrac{ v_t - v_{ p } }{ a_{ 2 } } = \dfrac{ ( 80 + 4 \sqrt{ 3 } ) \sqrt{ 3894550 - 436500 \sqrt{ 3 } } - 77600 - 3880 \sqrt{ 3 } } { 38509 } \mathrm{ s }。
故 t = t_{ 1 } + t_{ 2 } + t_{ 3 } \approx 6.92 \mathrm{ s }。
传送带上的滑痕长度即为滑块在与传送带共速前相对传送带运动的路程,即 \mathrm{ \Delta } x = \dfrac{ ( v_{ 0 } + v_{ p } )^{ 2 } }{ 2 a_{ 1 } } = \dfrac{ 9000 - 900 \sqrt{ 3 } }{ 97 } \mathrm{ m } \approx 76.61 \mathrm{ m }。
初始时滑块的动能 E_{ 1 } = \dfrac{ 1 }{ 2 } m v_{ 0 }^{ 2 },结束时滑块的动能 E_{ 2 } = \dfrac{ 1 }{ 2 } \lambda^{ \mathrm{ \Delta } x } m v_t^{ 2 }。
故 \gamma = \dfrac{ E_{ 2 } }{ E_{ 1 } } = \dfrac{ \lambda^{ \mathrm{ \Delta } x } v_t^{ 2 } }{ v_{ 0 }^{ 2 } } = \dfrac{ 0.99^\frac{ 9000 - 900 \sqrt{ 3 } }{ 97 } ( 4015 - 450 \sqrt{ 3 } ) } { 3880 } \times 100 \% \approx 38.57 \%。
综上,答案为:
- h = 17.05 \mathrm{ m };
- t = 6.92 \mathrm{ s };
- \mathrm{ \Delta } x = 76.61 \mathrm{ m };
- \gamma = 38.57 \%。
by ZHX。
