题目
令 f ( x ) = \dfrac{ \mathrm{ e }^{ x } - \mathrm{ e }^{ -x } + b }{ k },且 f ( x ) 为奇函数,且 f ( 1 ) = 1。
- 求 b, k。
- 求 g ( x ) = \dfrac{ f ( x ) }{ \mathrm{ e }^{ x } } 的值域。
- 直接写出 h ( x ) = f ( x ) - \mathrm{ e } x 的零点个数。
上述 \mathrm{ e } 均表示自然底数,约为 2.718282。
解析
-
因为 f ( x ) 为奇函数,且 f ( x ) 定义域为 \mathbb{ R },所以 f ( 0 ) = \dfrac{ b }{ k } = 0,即 b = 0。
因为 f ( 1 ) = \dfrac{ \mathrm{ e } - \dfrac{ 1 }{ \mathrm{ e } } }{ k } = 1,所以 k = \mathrm{ e } - \dfrac{ 1 }{ \mathrm{ e } }。
经检验,此时符合题目条件,故 b = 0, k = \mathrm{ e } - \dfrac{ 1 }{ \mathrm{ e } }。
-
g ( x ) = \dfrac{ 1 - \mathrm{ e }^{ -2 x } }{ k } = \dfrac{ 1 }{ k } - \dfrac{ \mathrm{ e }^{ -2 x } }{ k }。
因为 \mathrm{ e }^{ -2 x } 值域为 ( 0, +\infty ),故 -\dfrac{ \mathrm{ e }^{ -2 x } }{ k } 值域为 ( -\infty, 0 )。
故 g ( x ) 值域为 \left ( -\infty, \dfrac{ 1 }{ k } \right ),即 \left ( -\infty, \dfrac{ \mathrm{ e } }{ \mathrm{ e }^{ 2 } - 1} \right )。
-
共 3 个零点。
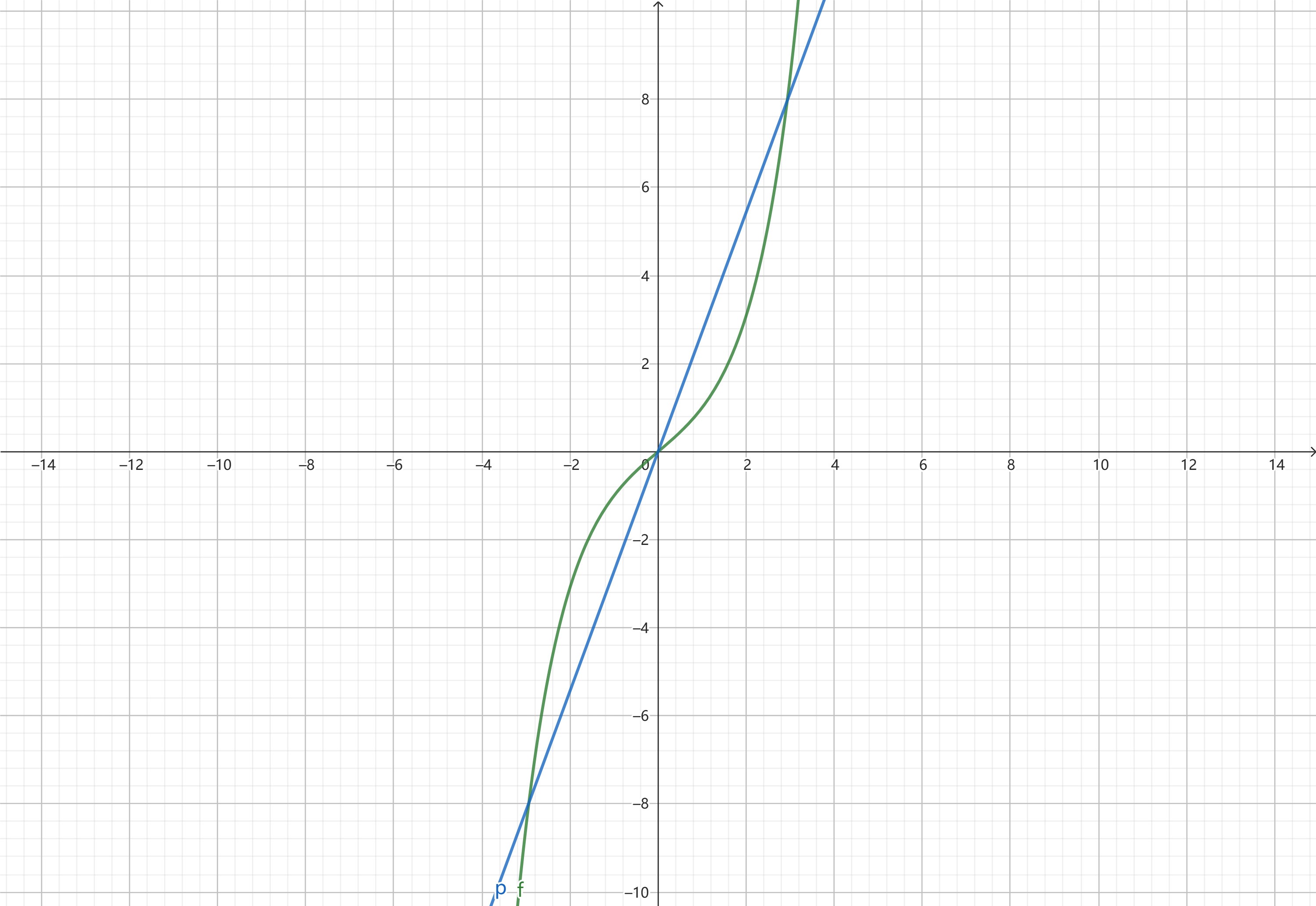
考虑 h ( x ) 的零点个数即为 f ( x ) 和 p ( x ) = \mathrm{ e } x 图像的交点个数。
绘制图像可发现共有 3 个交点(严格证明需要运用导函数结合零点存在定理,这里给出这三个交点的横坐标近似值,可代入计算器验证:-2.93367774, 0, 2.93367774)。
下面是 f ( x ) 和 p ( x ) 的示意图:
by CXY。
